Варто знати (повторити) ...
Вектор — це величина, яка характеризується числовим значенням і напрямком.
Під направленим відрізкомAB→ розуміють впорядковану пару точок, перша з яких — точка A — називається його початком, а друга — B — його кінцем. В геометрії розглядають вектори, що не залежать від точки прикладання (вільні вектори).
Графічно вектори зображають у вигляді направлених відрізків певної довжиниAB→ .
Поняття вектора з'явилося в роботах німецького математика XIX ст. Г. Грассмана та ірландського математика У. Гамільтона. Згодом воно було охоче сприйняте багатьма математиками і фізиками. В сучасній математиці це поняття відіграє дуже важливу роль.
Числа
ax=x2−x1,ay=y2−y1
називаються координатами вектораa⃗ з початком A(x1;y1) і кінцем B(x2;y2) .
(ax;ay)→.
a⃗ (ax;ay).
|a⃗ |=a2x+a2y−−−−−−√.
Сумою векторівa⃗ (ax;ay) і b⃗ (bx;by) називають вектор
c⃗ (ax+bx;ay+by).
Геометрично суму двох векторів можна знайти за:
Для складання двох векторів a⃗ і b⃗ за правилом трикутника обидва ці вектора переносяться паралельно самим собі так, щоб початок одного з них збігався з кінцем іншого. Тоді вектор суми задається третьою стороною трикутника, що утворився, причому його початок збігається з початком першого вектора.
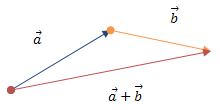
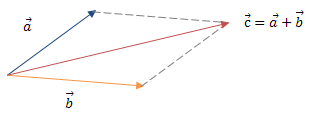
Для додавання двох векторів a⃗ і b⃗ за правилом паралелограма обидва ці вектора переносяться паралельно самим собі так, щоб їх початки збігалися. Тоді вектор суми задається діагоналлю побудованого на них паралелограма, яка виходить з їх спільного початку.
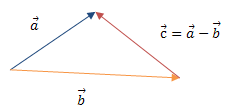
a⃗ і b⃗ називають такий вектор c⃗ , який в сумі з b⃗ дає a⃗ .
(ax;ay)→. на число λ називається вектор
(λax;λay)→.
axbx=ayby.
a⃗ ⋅b⃗ =ax⋅bx+ay⋅by.
a⃗ ⋅b⃗ =|a⃗ |⋅|b⃗ |⋅cos(a⃗ ;b⃗ ^). де (a⃗ ;b⃗ ^) — кут між векторами a⃗ і b⃗ .
Під направленим відрізком
Вектори позначають двома способами:
- малими буквами латинського алфавіту (наприклад,
a⃗ ); - двома великими буквами латинського алфавіту (наприклад,
AB→ ), де перша буква — початок вектора, а друга — кінець.
Графічно вектори зображають у вигляді направлених відрізків певної довжини
Рис. 1. Вектор AB з початком в A і кінцем в B
Поняття вектора з'явилося в роботах німецького математика XIX ст. Г. Грассмана та ірландського математика У. Гамільтона. Згодом воно було охоче сприйняте багатьма математиками і фізиками. В сучасній математиці це поняття відіграє дуже важливу роль.
Чисельне значенняa⃗ називається модулем чи довжиною і позначається|a⃗ | . Довжина вектора — це довжина відрізка, що зображає цей вектор.
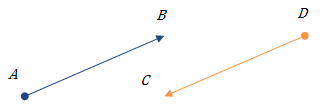
ВекториAB→ іCD→ називають протилежно напрямленими, якщо протилежно напрямлені півпряміAB іCD .
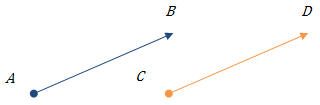
ВекториAB→ іCD→ називають співнапрямленими, якщо співнапрямлені півпряміAB іCD .

Рис. 3. Співнапрямлені вектори
Вектор, початок і кінець якого збігаються, називається нульовим і позначається0⃗ . Нульовий вектор має довжину 0. Напрям нульового вектора не визначений. Нульовий вектор прийнято рахувати співнапрямленим з будь-яким вектором. Вважається, що нульовий вектор одночасно паралельний і перпендикулярний будь-якому вектору.
Колінеарними називаються вектори, які зображаються відрізками, що лежать на одній прямій чи на паралельних прямих.
Два вектора називаються рівними, якщо вони однієї довжини і їх напрямки збігаються.
Одиничний вектор (орт) — вектор, довжина якого рівна одиниці.
Вектори на площині
Числа
називаються координатами вектора
Примітка 1. Всі координати нульового вектора дорівнюють нулю.
Примітка 2. Вектори рівні, коли їх відповідні координати рівні.
Вектор з координатамиax іay позначається
Векторa з координатамиax іay позначається
Використовуючи означення координат вектора довжину можна записати формулою
Дії над векторами на площині
Сумою векторів
Геометрично суму двох векторів можна знайти за:
- правилом трикутника;
- правилом паралелограма.
Правило трикутника
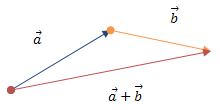
Рис. 4. Правило трикутника.
Правило паралелограма

Рис. 5. Правило паралелограма
Різницею векторів

Рис. 6. Різниця векторів
Добуток вектора
Два векториa⃗ іb⃗ колінеарні тоді і лише тоді, коли їх відповідні координати пропорційні
Скалярним добутком векторівa⃗ іb⃗
називається число, яке рівне сумі добутків відповідних координат, тобто
Скалярний добуток векторів дорівнює добутку їх довжин на косинус кута між ними, тобто